Potentiometrie
Dies ist eine Arbeit, die im Rahmen eines Uniprojektes entstanden ist und dient der Zusammenfassung und Erläuterung instrumenteller Analysemethoden in der Pharmazie. Konkret haben wir uns intensiv mit der Potentiometrie beschäftigt.
Titelblatt
Bericht der Expertengruppe für
Potentiometrie
SoSe 2021
Abgabedatum
19.06.2021
Über-/Expertengruppe 03
Max Brauer
Kilian Drotleff
Paul Gottschalk
Christopher Koop
Jan Maylahn
Benedict Sölter
Potentiometrie
Inhaltsverzeichnis
Einleitung
Die Potentiometrie beschäftigt sich mit der stromlosen Messung von Potentialdifferenzen zur Direktbestimmung vom pH-Wert und Ionenkonzentrationen oder Überwachung von Titrationsvorgängen. In beiden Fällen geschieht dies über die Messung der Potentialdifferenz zwischen einer Indikatorelektrode, die Elektronen je nach Redoxpotential auf den Analyten überträgt oder von ihm aufnimmt, und einer Bezugselektrode. Bei der potentiometrischen pH-Wert-Messung nehmen theoretisch H+-Ionen bzw. H2 den Platz der Analyten ein.
Physikalische und chemische Grundlagen der Potentiometrie
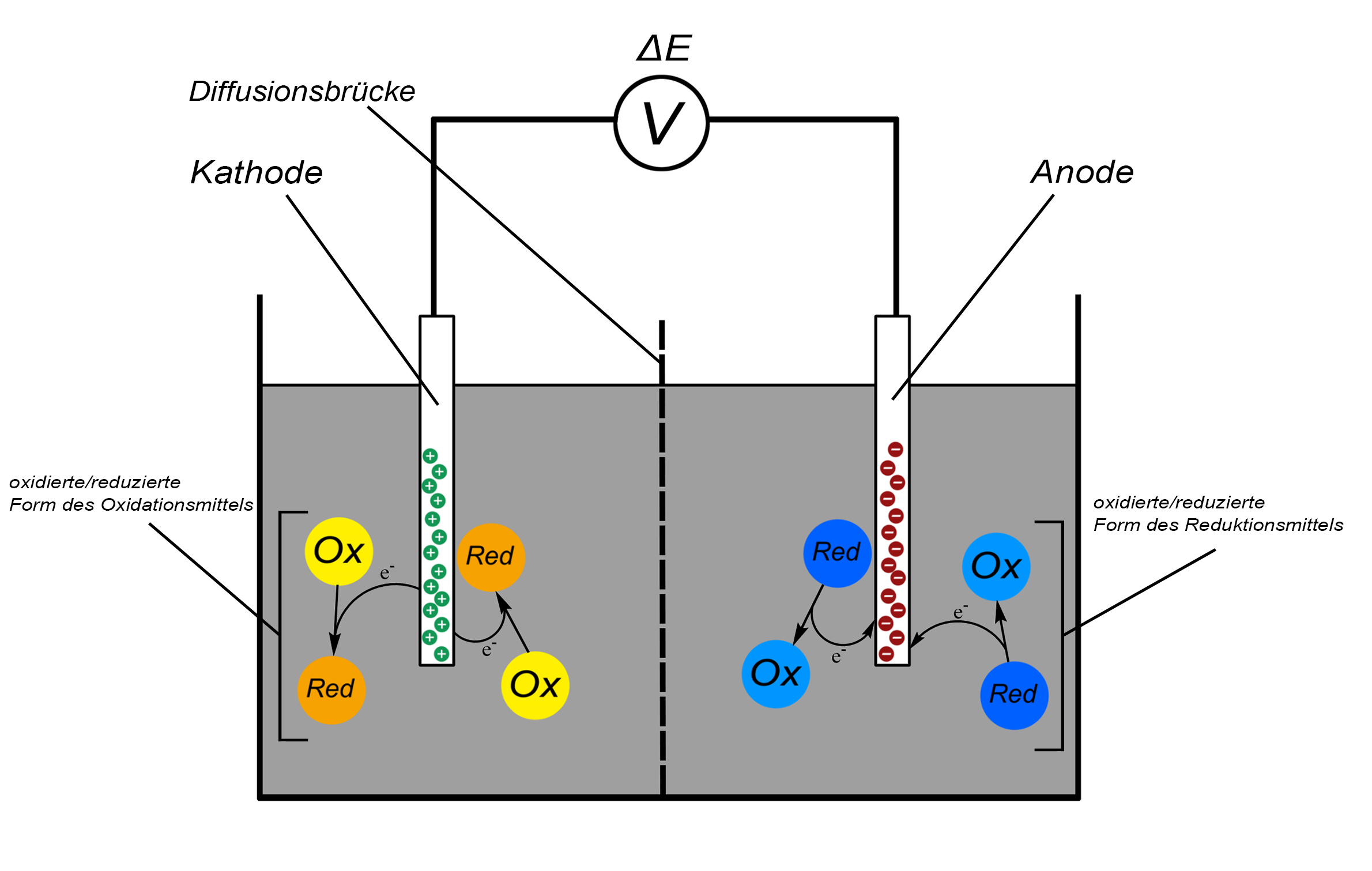
Aufbau einer galvanischen Zelle
Eine elektrochemische Potentialdifferenz ist eine Spannung zwischen zwei Elektroden, die gemessen werden kann, wenn diese in zwei räumlich getrennte Elektrolytlösungen getaucht werden. Das Elektrodenmaterial selbst oder Bestandteile der Lösung zeigen dann eine gewisse Bereitschaft zu oxidieren oder zu reduzieren. Elektronen werden dabei entweder in der Elektrode zurückgelassen oder von dieser aufgenommen. Diese Bereitschaft wird durch das elektrochemische Potential ⚠ $ E $ ausgedrückt und ist für jede Substanz spezifisch. Die Elektrode, in der Elektronen zurückgelassen wurden (Anode), trägt dadurch eine negative, während die, die Elektronen abgegeben hat, eine positive Ladung (Kathode) trägt.
Oxidation und Reduktion werden für eine potentiometrische Bestimmung räumlich getrennt, unter der Bedingung, dass beide Systeme durch eine Diffusionsbrücke (Salzbrücke, Diaphragma, o. Ä.) verbunden sind. In dem Fall spricht man von zwei Halbzellen, die zusammen eine galvanische Zelle bilden. Eine Halbzelle (Elektrode + Elektrolytlösung) besitzt also ein gewisses elektrochemisches Potential, welches allerdings nicht direkt gemessen werden kann. Zur Bestimmung wird deshalb die Potentialdifferenz ⚠ $ ΔE $ (Spannung) zwischen zwei verschiedenen Halbzellen gemessen. Diese Spannung wird auch als Leerlaufspannung oder Elektromotorische Kraft (⚠ $EMK$) bezeichnet.
Für genaue Messergebnisse muss allerdings ein stromloser Zustand vorliegen, da sich sonst die Konzentrationsverhältnisse in der Lösung bzw. direkt an der Elektrode während der Messung ändern. Daher kann es sinnvoll sein eine Poggendorff’sche Kompensationsschaltung einzusetzen. Hierbei wird genau die Potentialdifferenz (Leerlaufspannung) der Halbzellen entgegengesetzt angelegt, so dass es zu keinem Stromfluss kommt. Gemessen wird dann die entgegengesetzte Spannung. Moderne Spannungsmessgeräte weisen einen sehr hohen Widerstand (>1012 Ω) auf, welche einen Elektronenfluss weitestgehend verhindern und somit eine hinreichende Genauigkeit garantieren können. Allerdings besteht zwischen den beiden Elektrolytlösungen ein “Diffusionsdruck”, der durch unterschiedlich große Permeabilitäten der Ionen an der Grenze zwischen den Halbzellen (bspw. Diaphragma) und den dadurch resultierenden Konzentrationsunterschieden bedingt ist, und sich in Form des Diffusionspotentials ⚠ $U_D $ äußert. Dieses Diffusionspotential kann die Messergebnisse stören, ist aber unter Standardbedingungen konstant.
Das Ausmaß, in dem die Redoxvorgänge geschehen, hängt von der jeweiligen Substanz, deren Konzentrationen der oxidierten bzw. reduzierten Form und der Temperatur ab. Der Einfluss der Konzentrationen wird durch das Massenwirkungsgesetz beschrieben. Findet diese Messung unter Standardbedingungen (25°C, 1013 hPa, alle Aktivitäten = 1) statt, wobei an einer Elektrode H2 bzw. H+ als Referenz umgesetzt wird, handelt es sich um das Standardpotential. Die Abhängigkeiten des Standardpotentials werden in der Nernst-Gleichung zusammengefasst:
⚠ $$ E = E_0 + \frac{R \cdot T}{F \cdot z^*} \cdot ln \frac{a_{ox}}{a_{red}} ⚠ $$
(Gl. 1)
Die absolute Temperatur ⚠ $ T $, die Gaskonstante ⚠ $ R $ sowie die Faraday-Konstante ⚠ $ F $ können mit dem Faktor 2,303 (Umwandlung vom natürlichen zum dekadischen Logarithmus) zu einer Konstanten ⚠ $ f $ von ca. 0,059 V bei 25°C zusammengefasst werden. Außerdem werden annäherungsweise die Stoffmengenkonzentration der entsprechenden Substanzen anstatt deren Aktivitäten betrachtet. Dadurch erhält man eine handlichere Gleichung:
⚠ $$ \\ E = E_0 + \frac{0,0591V}{z^*} \cdot lg \frac{c_{ox}}{c_{red}} ⚠ $$
(Gl. 2)
Die theoretische Potentialdifferenz zwischen den zwei Halbzellen wird nun nach folgender Gleichung berechnet:
⚠ $$ \Delta E = E_{Kathode} - E_{Anode} = \left[ E_0 (Oxidationsmittel) + \frac{0,0591V}{z^*} \cdot lg \frac{c_{ox}}{c_{red}} \right] - \left[ E_0 (Reduktionsmittel) + \frac{0,0591V}{z^*} \cdot lg \frac{c_{ox}}{c_{red}} \right] ⚠ $$
(Gl. 3)
Direktpotentiometrie
Bei der Direktpotentiometrie wird die Konzentration eines Analyten in Lösung bestimmt, indem die Spannung zwischen der Indikatorelektrode, an welcher der Analyt umgesetzt wird, und einer Bezugselektrode gemessen wird. Mithilfe der Nernst-Gleichung lässt sich dann aus der Leerlaufspannung die Konzentration des Analyten errechnen.
Die Leerlaufspannung setzt sich unter Berücksichtigung des Diffusionspotential
(⚠ $U_D $) wie folgt zusammen:
⚠ $$ U = U_{Ind} - U_{Bez} + U_D ⚠ $$
Um die Konzentration der Analytlösung zu bestimmen wird die Nernst-Gleichung für ⚠ $U_{Ind} $ und ⚠ $U_{Bez} $ eingesetzt (vgl. Gl. 3). Diese Gleichung lässt sich bei konstanter Ionenstärke vereinfachen, indem die konstanten Werte ⚠ $ U_{Bez} $, ⚠ $ U_D $ und ⚠ $ E_0 $ zu einer Konstanten ⚠ $ K $ zusammengefasst werden. Eine weitere Annahme, die getroffen werden muss, ist, dass die Aktivität des Analyten der Konzentration entspricht. Wenn die betrachtete Indikatorelektrode die Kathode ist, also die oxidierte Spezies in Lösung betrachtet wird, wird ⚠ $ c_{red} = 1 $ angenommen, da diese meist als feste oder gasförmige Phase auftritt.
⚠ $$ U = K + \frac{0,0591 V}{z^*} \cdot lg (c) ⚠ $$
Umgekehrt gilt, dass wenn die Indikatorelektrode die Anode ist, also die reduzierte Spezies in Lösung betrachtet wird, ist ⚠ $ c_{ox} = 1 $ und die gesuchte Analytkonzentration befindet sich nun im Nenner des logarithmischen Ausdrucks.
Es ist nicht auszuschließen, dass sich in der Untersuchungslösung weitere elektrochemisch-aktive Substanzen befinden, welche die Messung stören. Aus diesem Grund können ionenselektive Elektroden Anwendung finden, die die Störeffekte reduzieren. 1
Potentiometrische Titration
Bei der potentiometrischen Titration wird der Fortschritt der Titration durch eine Potentialänderung der Analytlösung überwacht.
Vor Zugabe der Maßlösung ist das Potential der Lösung ausschließlich auf den Analyten zurückzuführen. Dieser wird im Laufe der Titration durch die Maßlösung umgesetzt, wodurch sich das Konzentrationsverhältnis von oxidierter zu reduzierter Spezies ändert (s. Nernst-Gleichung). Die Maßlösung selbst hat zu diesem Zeitpunkt keinen Einfluss auf das Potential, da diese bis zum Äquivalenzpunkt nahezu vollständig umgesetzt wird:
⚠ $$ E = E_0(A) + \frac{0,0591V}{z^*(A)} \cdot lg \left(\frac{\tau}{1-\tau}\right) ⚠ $$
Am Äquivalenzpunkt ist ein Potential messbar, welches dem arithmetischen Mittelwert der Standardpotentiale von Analyt (⚠ $ E_0(A) $) und Maßlösung (⚠ $ E_0(ML) $) entspricht, es sei denn die Umsetzung erfolgt nicht mit äquimolaren Mengen an Analyt und Maßlösung. In dem Fall werden die besagten Standardpotentiale unterschiedlich stark gewichtet:
⚠ $$ E_{Äq} = \frac{E_0(A) \cdot z^*(A) + E_0(ML) \cdot z^*(ML)}{z^*(A) + z^*(ML)} ⚠ $$
Sind an der Teilreaktion der Maßlösung Protonen beteiligt, hat zusätzlich der pH-Wert der Lösung sowie die stöchiometrische Anzahl der beteiligten Protonen (⚠ $ y $) einen Einfluss auf das Potential der Lösung am Äquivalenzpunkt:
⚠ $$ E_{Äq} = \frac{E_0(A) \cdot z^*(A) + E_0(ML) \cdot z^*(ML) - 0,0591V \cdot y \cdot pH}{z^*(A) + z^*(ML)} ⚠ $$
Bei weiterer Zugabe von Maßlösung über den Äquivalenzpunkt hinaus ist das Potential ausschließlich auf die Maßlösung zurückzuführen:
⚠ $$ E = E_0(ML) + \frac{0,0591V}{z^*(ML)} \cdot lg (\tau - 1) ⚠ $$
Auch hier kann der pH-Wert einen Einfluss haben, wenn an der Umsetzung der Maßlösung Protonen beteiligt sind: 2
⚠ $$ E = E_0(ML) + \frac{0,0591V}{z^*(ML)} \cdot \left[ lg (\tau - 1) - y \cdot pH \right] ⚠ $$
Instrumenteller Aufbau
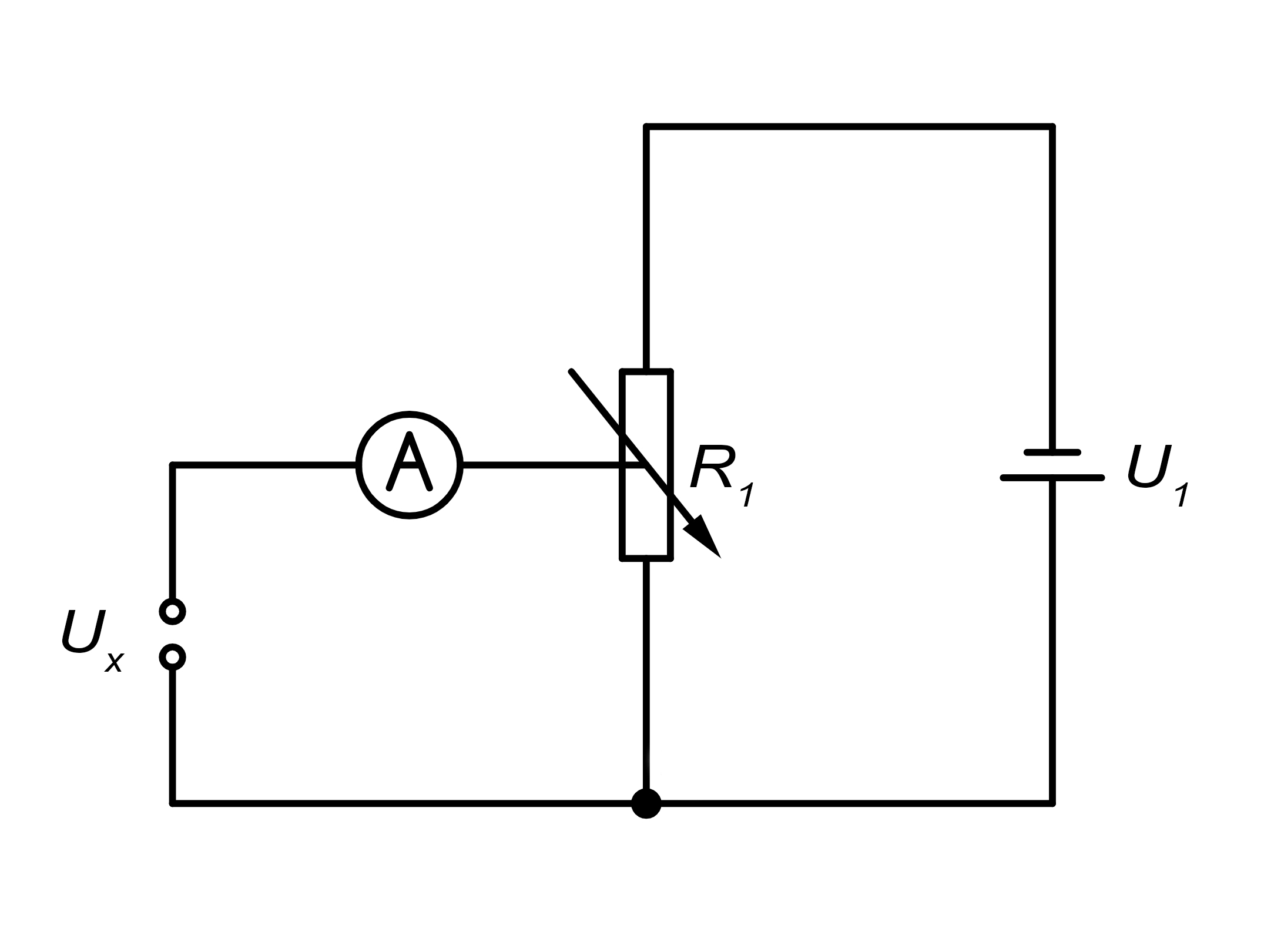
Schaltbild für eine stromlose Messung.
Messanordnung für potentiometrische Titration
Durchführung einer stromlosen Messung
Bei der Poggendorff'schen Kompensationsmethode wird die Forderung der Stromlosigkeit erfüllt, indem man die Leerlaufspannung durch eine gleichgroße Spannung kompensiert. Die Kompensationsspannung U1 ist der zu messenden Spannung Ux entgegengesetzt und wird durch den variablen Widerstand R1 (Potentiometer) reguliert. U1 ist in diesem Aufbau konstant und wird durch den Widerstand R1 verändert. Das Amperemeter zeigt die absolute Stromlosigkeit an, sobald diese erreicht ist. Anhand des eingestellten Widerstandes kann man auf die Spannung Ux schließen, da diese genau so groß ist wie die Kompensationsspannung UK, die durch den variablen Widerstand eingestellt wurde.3
Aktuelle Messgeräte für potentiometrische Titration
Moderne Messgeräte (Voltmeter) sind sehr hochohmig, sodass für eine hinreichende Genauigkeit der Innenwiderstand des Messgerätes ausreicht. Heutzutage kann daher auf die Poggendorff'sche Kompensationsmethode verzichtet werden.
Unterscheidung von Elektroden
Man unterscheidet bei der Potentiometrie zwischen Bezugselektroden und Messelektroden. Dabei kommen Elektroden 1., 2. und 3. Art zum Einsatz. Während bei der Elektrode 1. Art ein Ion beteiligt ist, sind bei den Elektroden 2. und 3. Art zwei bzw. drei Ionen am potentialbildenden Schritt beteiligt. Durch den unterschiedlichen Aufbau haben die jeweiligen Elektroden auch unterschiedliche Funktionen.
Bezugs-/Referenz-/Vergleichselektroden
Eine Bezugselektrode ist eine Halbzelle mit einem konstanten Potential, welches sich in der Praxis gut reproduzieren lässt.
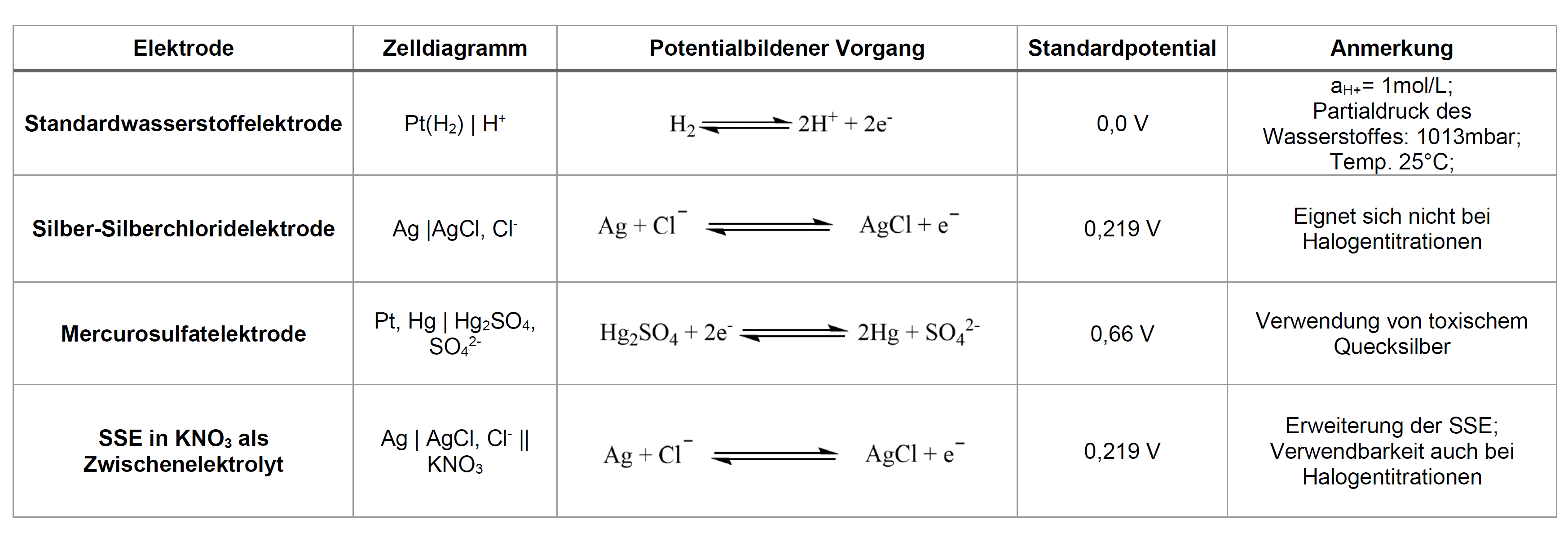
1. Standardwasserstoffelektrode (SHE)
Dem Aufbau der Standardwasserstoffelektrode zugrunde liegend ist ein Glasbehälter, welcher sauerstofffrei gehalten werden muss, um eine Knallgasreaktion zwischen dem Wasserstoffgas der Elektrode und Sauerstoff aus der Umgebungsluft zu vermeiden. Der Glasbehälter ist mit einer salzsauren Lösung mit einer Ionenaktivität der Wasserstoff-Ionen von aH+ = 1 mol/L gefüllt, in der ein platiniertes Platinblech taucht. Dieses Blech wird umspült von Wasserstoffgas unter Normalbedingungen, welches an der Metalloberfläche adsorbiert und das Blech so mit einer dünnen Schicht aus Wasserstoff umgibt. Der potentialbildene Vorgang lautet:
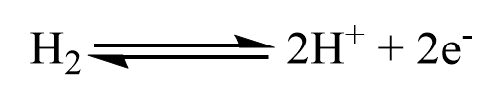
Die Standardwasserstoffelektrode dient zunächst wie jede Bezugselektrode dem Zweck, ein genau definiertes Potential zu liefern. Darüber hinaus ist sie zur Bestimmung von Standardpotentialen geeignet, da ihr Potential definitionsgemäß der Nullpunkt der Standardpotentialskala ist. Weil der komplexe Aufbau allerdings die Verwendung von gasförmigen Wasserstoff voraussetzt, welches zudem Knallgasreaktionen hervorrufen kann und eine ständige Druckkontrolle erfordert. Deshalb die Standardwasserstoffelektrode heutzutage zu Forschungszwecken äußerst selten verwendet. Deutlich unproblematischer gestaltet sich bspw. die Verwendung einer Silber-Silberchloridelektrode.4
2. Silber-Silberchloridelektrode (SSE)
Hierbei handelt es sich um eine Elektrode 2. Art. Ein mit Silberchlorid bedeckter Silberdraht taucht in einer chloridhaltigen Lösung (meist eine gesättige Kaliumchlorid-Lösung). Über ein Diaphragma wird ein minimaler Ionenfluss zwischen der Elektrode und der umgebenden Probelösung gewährleistet, der ausreicht, um ein Redoxgleichgewicht einzustellen. Das Potential der Elektrode ist allein abhängig von der Aktivität der zugesetzten Elektrolytlösung [hier: Kaliumchlorid]. Der potentialbildene Schritt ist die Oxidation von Silber zu Silberchlorid.

Die dazugehörige Nernstgleichung lautet:
⚠ $$ E = E^0_{Ag/Ag^+} + {0,0591V \over z^*} \cdot \lg\; a{\mathrm(Ag^+)} ⚠ $$
Das Löslichkeitsprodukt von Silberchlorid lässt sich durch folgende Gleichung ausdrücken:
⚠ $$ K_L = a_{eq}\mathrm(Ag^+) \cdot a_{eq}\mathrm(Cl^-) ⚠ $$
Eingesetzt in die Nernstgleichung und vereinfacht ergibt sich folgende Gleichung:
⚠ $$ E = E^0_{Ag/AgCl} - {0,0591V \over z^*} \cdot \lg\; a{\mathrm(Cl^-)} ⚠ $$
Da der Kaliumchlorid-Lösung der SSE auch feste Kaliumchlorid-Kristalle hinzugefügt werden, kann ein Verlust von Chlorid-Ionen an die Probelösung ausgeglichen und die Konzentration der Chlorid-Ionen so ebenfalls konstant gehalten werden. Auf diese Weise wird das genau definierte Potential von 0,219 V erreicht. Aufgrund dieser Eigenschaft und der vergleichsweise leichten Handhabung ist die Silber-Silberchloridelektrode eine häufig gewählte Bezugselektrode. 5,6
3. Mercurosulfatelektrode (MSE)
Bei der Mercurosulfatelektrode handelt es sich um eine chloridfreie Bezugselektrode, welche dann Einsatz findet, wenn die Chlorid-Ionen der SSE den Vorgang in der Probelösung beeinflussen könnten, was z. B. bei einer Halogentitration der Fall ist. Da die Elektrode Quecksilber benötigt, ist die Verwendung heutzutage nur noch sehr selten vorzufinden. Stattdessen wird meistens eine SSE in Kaliumnitrat-Lösung als Zwischenelektrolyt verwendet. Der potentialbildene Vorgang ist die Reduktion von Quecksilbersulfat:
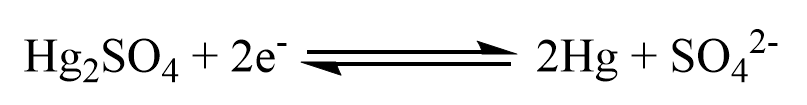
Das Zelldiagramm der Mercurosulfatelektrode lautet:
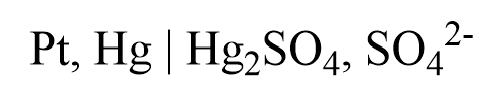
Eine Elektrode, die ebenfalls Quecksilber beinhaltet, ist die gesättigte Kalomelelektrode. Diese unterscheidet sich von der Mercurosulfatelektrode nur insofern, dass Chlorid-Ionen anstelle von Sulfat-Ionen als Gegenion verwendet werden.7
4. SSE in Kaliumnitrat-Lösung als Zwischenelektrolyt
Durch die Verwendung eines Zwischenelektrolyten, wie Kaliumnitrat-Lösung, kann die SSE auch bei Halogentitrationen verwendet werden, bei der Chlorid stören würde, da die Kaliumchlorid-Lösung räumlich von der Probelösung getrennt ist. Der potentialbildene Vorgang unterscheidet sich nicht von dem der SSE. Das Zelldiagramm lautet:8
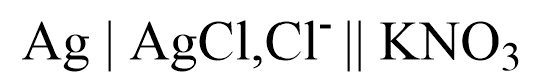
Indikator-/Messelektroden
1. Redox-Elektroden
Redox-Elektroden nehmen nicht am potentialbildenen Vorgang teil, sondern leiten das Potential des in Lösung befindlichen Redox-Systems ab. Deshalb bezeichnet man diese Elektroden auch als Ableitelektroden. Weil die Elektroden nicht selbst an der Reaktion teilnehmen sollen, müssen diese aus einem inertem Material bestehen. Häufig werden Platin, Gold oder Kohlenstoff verwendet.9
2. pH-sensitive Elektroden
Dies sind Elektroden, die auf eine Änderung des pH-Wertes mit einer Potentialänderung reagieren.
2.1. Chinhydronelektrode
In die Messlösung wird eine Spatelspitze Chinhydron (Hydrochinon + Chinon im Verhältnis 1:1) gemischt und ein Platindraht als Ableitelektrode gehängt. Je nach pH-Wert liegt entweder Chinon oder Hydrochinon überwiegend vor. Da sich hierbei das Potential ändert, kann auf den pH-Wert geschlossen werden. Der potentialbildene Vorgang an der Platinelektrode lautet:
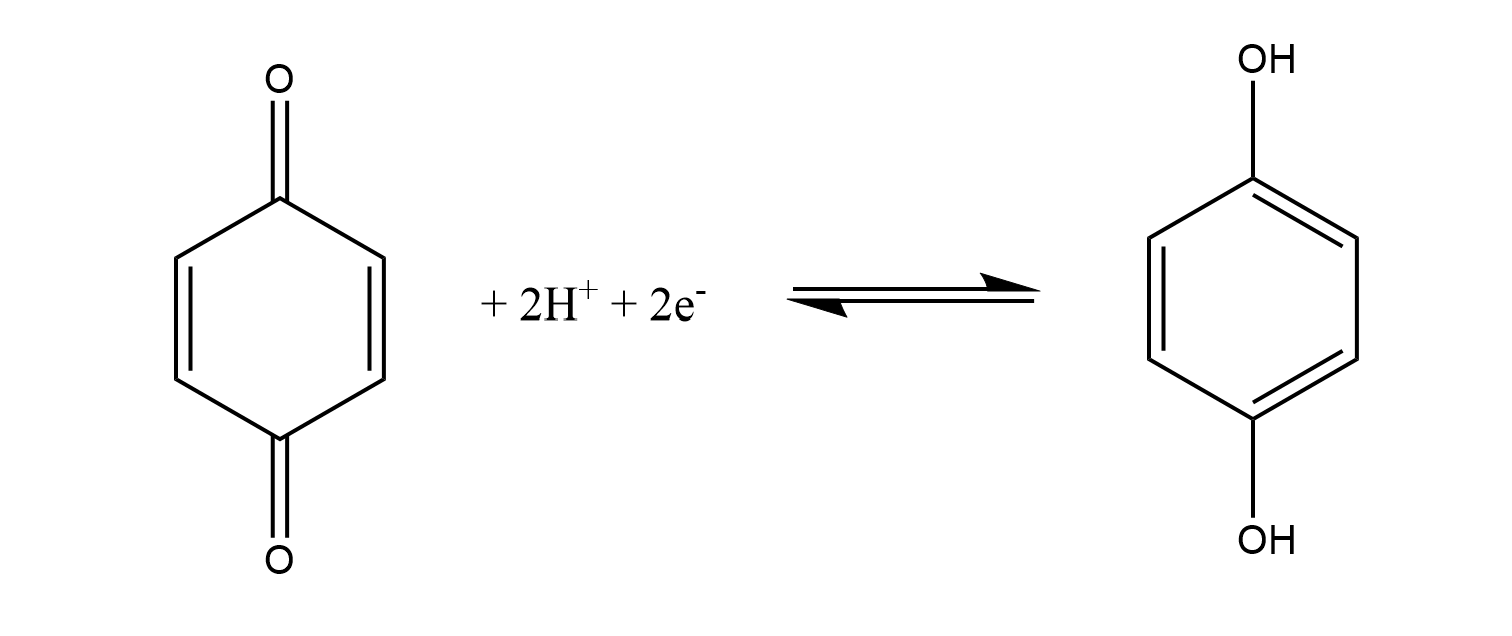
Somit lautet das Zelldiagramm mit einer SSE als Bezugselektrode:
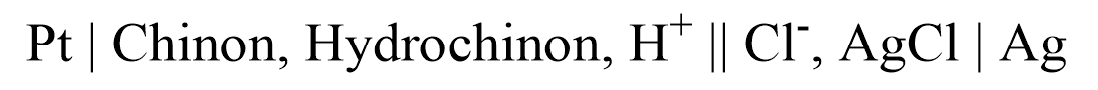
Der Anwendungsbereich ist allerdings begrenzt auf den pH-Bereich von 0-8, da bei pH > 8 das Hydrochinon deprotoniert wird. Außerdem dürfen in der zu analysierenden Lösung keine Oxidations- und Reduktionsmittel vorhanden sein, da diese das Potential verändern würden. Deshalb wird häufiger die Glaselektrode verwendet.10,11
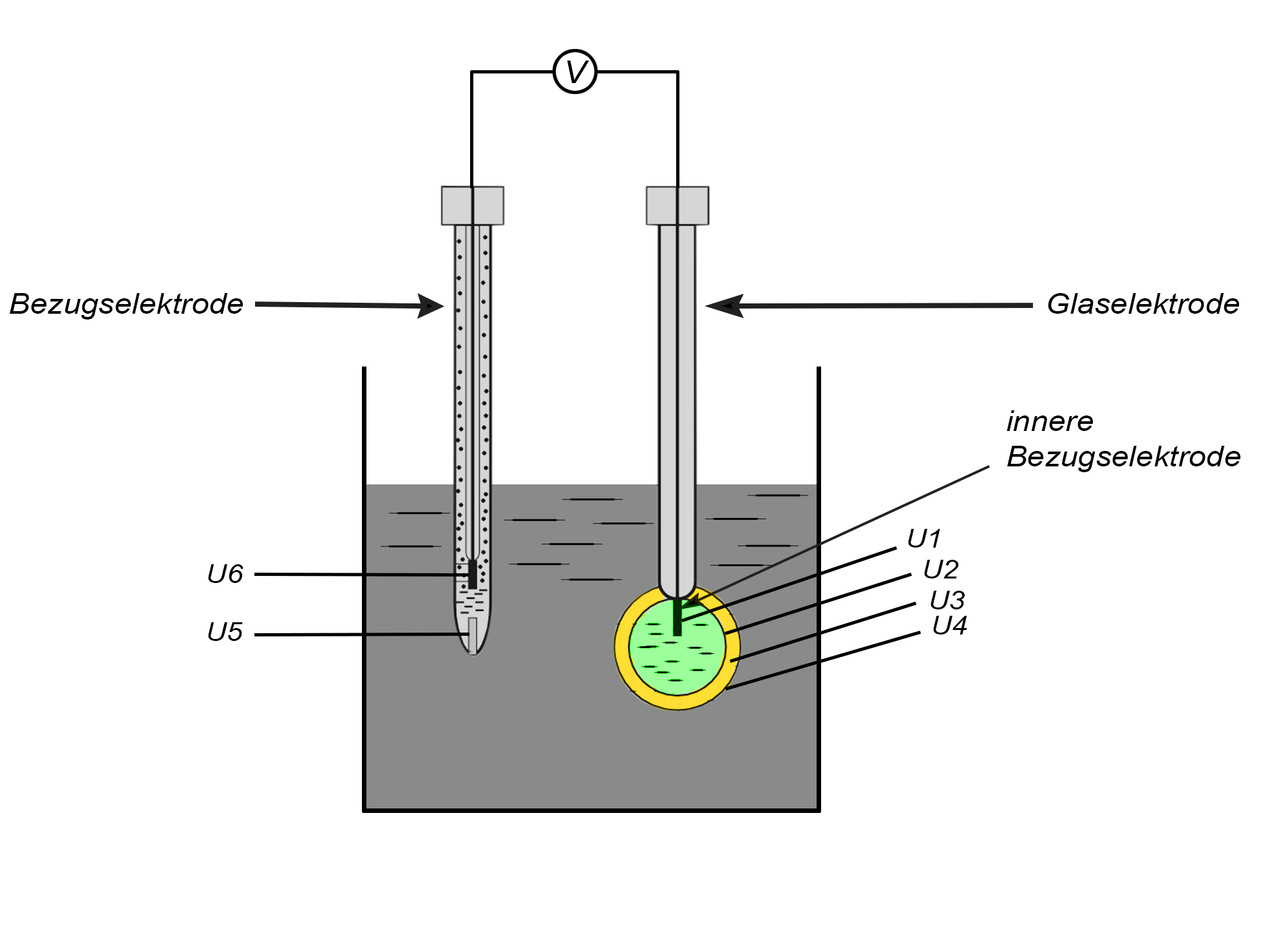
2.2. Glaselektrode
Die Glaselektrode ist aufgrund der einfachen und präzisen Handhabung eine der am häufigsten eingesetzten pH-Elektroden in der instrumentellen Analytik. Außerdem eignet sich die Elektrode sowohl für die Analyse von wässrigen Proben als auch von nicht-wässrigen Proben. Glaselektroden können als "klassische galvanische Zellen", deutlich häufiger aber als Einstabmessketten eingesetzt werden. Der Aufbau ist komplexer als bei anderen Elektroden. Entscheidend für die Funktionsweise ist eine sehr dünne kugelförmige Glasmembran, welche in die Untersuchungslösung eingetaucht wird. In dieser Kugel befindet sich eine innere Bezugselektrode, welche als Ableitelektrode dient. Meistens handelt es sich um eine SSE. Die Glaskugel ist gefüllt mit einer Kaliumchlorid-Lösung, welche auf pH = 7 gepuffert ist. Diese dient als Kalibrierlösung.
Die Funktionsweise der pH-abhängingen Potentialänderung beruht auf Austauschgleichgewichten von Alkali-Ionen der Glasmembran und Protonen der Messlösung. Außerdem ist eine weitere Bezugselektrode notwendig - in der Regel ebenfalls eine SSE. Das Zelldiagramm lautet:
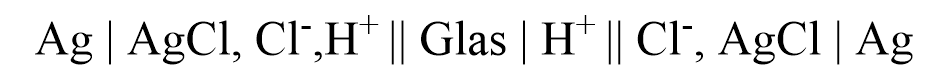
Die beiden Referenzelektroden (SSEs) messen die elektrische Potentialdifferenz an der Glasmembran. Das Silikatgitter im Glas weist eine unregelmäßige Struktur auf und negativ geladene Sauerstoffatome können Metallkationen geeigneter Größe binden. Natrium-Ionen können langsam durch das Glas diffundieren.
Diese Vorgänge laufen in der inneren und der äußeren Quellschicht der Glasmembran ab. Die ausgebildeten Potentialdifferenzen lassen sich durch die Nernstgleichung beschreiben. Um einen Spannungsabfall in der Glasmembran zu vermeiden, muss der Innenwiderstand des äußeren Messgerätes extrem hochohmig sein. Insgesamt treten verschiedene Potentialdifferenzen auf:
U1: Potentialdifferenz der inneren Bezugselektrode
U2: Potentialdifferenz an der inneren Zellgrenze zwischen Glasmembran und KCl-Lösung
U3: Asymmetriepotential durch unterschiedliche Dicken der Glasmembran
U4: Potentialdifferenz an der äußeren Zellgrenze zwischen Glasmembran und Messlösung
U5: Diffusionspotential am Diaphragma der Bezugselektrode
U6: Potentialdifferenz der Bezugselektrode
Das theoretisch gemessene Gesamtpotential setzt sich aus den Potentialen U1, U2, U4, U6 zusammen. Die Potentiale U3 und U5 treten als Störpotentiale auf.
Die Spannung der Ableitelektrode und der Bezugselektrode kompensieren sich aufgrund des identischen Aufbaus zu null. Das Potential an der inneren Zellgrenze zwischen der Glasmembran und Kaliumchlorid-Lösung ist wegen der übersättigten Kaliumchlorid-Lösung ebenfalls konstant. Somit ist die messbare Potentialdifferenz nur noch vom variablen pH-Wert der Messlösung abhängig. Durch die Änderung der Potentialdifferenz an der äußeren Glasmembran ändert sich die Gesamtpotentialdifferenz. Diese Potentialdifferenz ist nun theoretisch linear abhängig vom pH-Wert über den gesamten Messbereich von 0-14. In stark sauren Lösungen kann eine Querempfindlichkeit gegenüber Anionen auftreten, was zum sogenannten Säurefehler führt. In stark alkalischen Lösungen kann es zu einer Querempfindlichkeit gegenüber Alkali-Ionen kommen. Dabei sind es nicht die Hydroxid-Ionen, sondern die Alkali-Ionen, die den Alkali-Fehler verursachen. Das Asymmetriepotential, welches durch unterschiedliche Quellungen bedingt ist, sorgt ebenfalls für Abweichungen. Deshalb muss die Elektrode kalibriert werden.14,15
3. Ionenselektiver Feldeffekttransistor (ISFET)
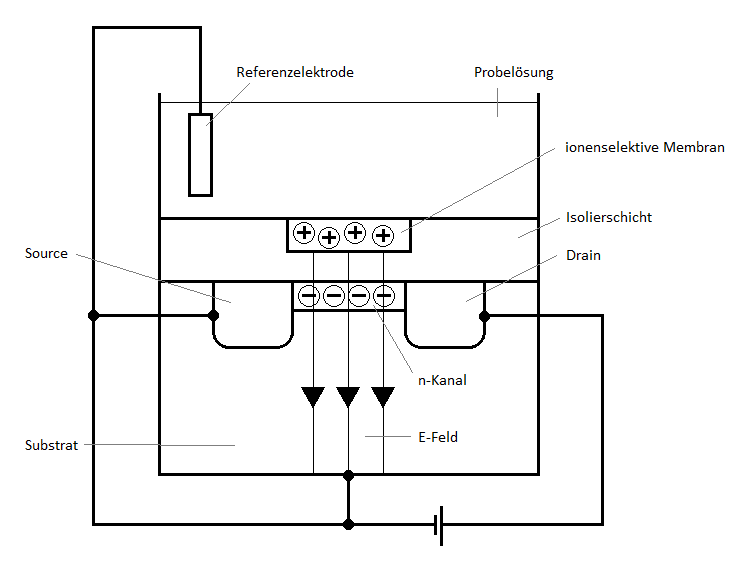
Schematischer Aufbau eines ISFETs zur Messung des pH-Wertes.
Bei diesem Spezialfall einer Messelektrode handelt es sich um einen Feldeffekttransistor, welcher in der Lage ist, die Konzentration eines spezifischen Ions zu messen. Abwandlungen des ISFETs sind in der Biomedizin weit verbreitet und sind beispielsweise in der Lage, die Konzentration bestimmter Enzyme oder Kohlenhydrate zu messen. Seine Größe liegt typischerweise im Mikrometerbereich. Im Folgenden wird der grundlegende Aufbau des ISFETs anhand des Beispiels einer pH-Messung erläutert. 16
Das Ausgangsmaterial des ISFETs ist ein Halbleiter, meist ein Siliciumkristall. Hier sind zunächst alle Valenzelektronen an den Bindungen zu benachbarten Siliciumatomen beteiligt. Erst wenn dem Halbleiter (durch Wärme oder Photonen) Energie zugeführt wird, werden einige der Valenzelektronen von ihrem Grundenergieniveau, welches auch Valenzband genannt wird, in das energetisch höherliegende Leitungsband angeregt. Die Elektronen im Leitungsband sind frei beweglich, und hinterlassen an ihrem Ursprungsort einen Ort mit formeller positiver Ladung, ein sogenanntes Loch. Rückt nun ein anderes Elektron an diesen Platz und gleicht die positive Ladung aus, so bleibt an dessen Ursprungsort wiederum ein Loch zurück.
Die Anzahl an Leitungsbandelektronen oder Löchern im Halbleiter kann auch durch eine Dotierung, also die Einführung von Fremdatomen in den Siliciumkristall manipuliert werden. Das Substrat des ISFETs ist p-dotiert, das heißt einige der Gitteratome wurden durch Atome mit weniger Valenzelektronen als Silicium, wie Bor oder Aluminium ersetzt, wodurch das Substrat eine Überzahl an Löchern besitzt. Die beiden Inseln im oberen Bereich des Halbleitermaterials – Source und Drain – sind dagegen n-dotiert. Hier sind einige der Gitteratome durch Atome mit zusätzlichen Valenzelektronen, wie z. B. Phosphor ersetzt worden, sodass ein Überschuss an Leitungsbandelektronen existiert. Im Grenzbereich zwischen p- und n-dotierten Bereichen werden Teile der Leitungsbandelektronen und Löcher auf die gegenüberliegende Seite diffundieren und dort miteinander rekombinieren; es entsteht eine isolierende Verarmungszone mit neutraler Raumladung. Aus diesem Grund kann ohne Weiteres kein Strom zwischen Source und Drain fließen. 17
Oberhalb dieses Bereichs befindet sich die zu analysierende Probelösung, welche durch eine isolierende Siliciumdioxid-Schicht vom Halbleitermaterial getrennt ist. In der Nähe der n-dotierten Bereiche befindet sich eine ionenselektiven Membran, in der sich H+-Ionen aus der Probelösung sammeln. Da der „Boden“ des Substrats mit einer Stromquelle verbunden ist und daher ein negatives Potential besitzt, entsteht nun nach dem Prinzip eines Plattenkondensators ein elektrisches Feld (E-Feld) zwischen der ionenselektiven Membran und dem Substrat. Dieses E-Feld bewirkt, dass Leitungsbandelektronen aus dem Substrat in Richtung der ionenselektiven Membran bewegt werden. Wenn nun genügend Elektronen angezogen werden, sodass die Löcher im Bereich zwischen Source und Drain ausgeglichen werden und sich anschließend ein Überschuss an Elektronen bildet, entsteht ein leitender n-Kanal, der Source und Drain miteinander verbindet, und damit auch ein geschlossener Stromkreis. Die Leitfähigkeit des n-Kanals hängt direkt von der elektrischen Feldstärke dieses E-Feldes und damit von der Konzentration der H+-Ionen in der Probelösung ab. Eine Referenzelektrode, welche ebenfalls in der Probelösung taucht, leitet das Potential der Lösung weiter. Aus der Potentialdifferenz, die dann zwischen der Lösung und dem Halbleiter gemessen wird, kann der pH-Wert der Probelösung berechnet werden. 18,19
Einzelnachweise
1 Rücker, G., Neugebauer, M. & Willems, G. G.(2013). Instrumentelle Pharmazeutische Analytik. Stuttgart, Germany: Wissenschaftliche Verlagsgesellschaft Stuttgart, S.553ff ⇑
2 Quantitative Bestimmung von Arznei-, Hilfs- und Schadstoffen, Grünefeld, J., 2020, Seite 59ff ⇑
3 Müller U. (2010). Physikalisches Grundpraktikum. Abgerufen am 25.05.2021, von https://gpr.physik.hu-berlin.de/Skripten/Elektrodynamik%20und%20Optik/PDF-Dateien/E7.pdf ⇑
4 Einführung in die Instrumentelle Analytik: Elektrochemische Methoden, Orban, O., 2020, Folie 34 f ⇑
5 Rücker, G., Neugebauer, M. & Willems, G. G.(2013). Instrumentelle Pharmazeutische Analytik. Stuttgart, Germany: Wissenschaftliche Verlagsgesellschaft Stuttgart, S.529f ⇑
6 Einführung in die Instrumentelle Analytik: Elektrochemische Methoden, Orban, O., 2020, Folie 36ff ⇑
7 Einführung in die Instrumentelle Analytik: Elektrochemische Methoden, Orban, O., 2020, Folie 39 ⇑
8 Einführung in die Instrumentelle Analytik: Elektrochemische Methoden, Orban, O., 2020, Folie 39 ⇑
9 Rücker, G., Neugebauer, M. & Willems, G. G.(2013). Instrumentelle Pharmazeutische Analytik. Stuttgart, Germany: Wissenschaftliche Verlagsgesellschaft Stuttgart, S.532 ⇑
10 Rücker, G., Neugebauer, M. & Willems, G. G.(2013). Instrumentelle Pharmazeutische Analytik. Stuttgart, Germany: Wissenschaftliche Verlagsgesellschaft Stuttgart, S.533 ⇑
11 Einführung in die Instrumentelle Analytik: Elektrochemische Methoden, Orban, O., 2020, Folie 41 ⇑
12 Von Glaselektrode_Schematischer_Aufbau.png: Der ursprünglich hochladende Benutzer war SusanW in der Wikipedia auf Deutschderivative work: Matt (talk) - Glaselektrode_Schematischer_Aufbau.png, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=11168656 ⇑
13 Abbildung nach: Rücker, G., Neugebauer, M. & Willems, G. G.(2013). Instrumentelle Pharmazeutische Analytik. Stuttgart, Germany: Wissenschaftliche Verlagsgesellschaft Stuttgart, S.556 ⇑
14 Rücker, G., Neugebauer, M. & Willems, G. G.(2013). Instrumentelle Pharmazeutische Analytik. Stuttgart, Germany: Wissenschaftliche Verlagsgesellschaft Stuttgart, S.555ff ⇑
15 Einführung in die Instrumentelle Analytik: Elektrochemische Methoden, Orban, O., 2020, Folie 42ff ⇑
16 Schöning, M., Poghossian, A., (2002). Recent advances in biologically sensitive field-effect transistors(BioFETs). Abgerufen am 06.06.2021, von https://juser.fz-juelich.de/record/16078/files/12968.pdf ⇑
17 Rücker, G., Neugebauer, M. & Willems, G. G.(2013). Instrumentelle Pharmazeutische Analytik. Stuttgart, Germany: Wissenschaftliche Verlagsgesellschaft Stuttgart, S.562f ⇑
18 International Union of Pure and Applied Chemistry (2016). Ion-selective field effect transistor (ISFET) devices. Abgerufen am 06.06.2021, von http://publications.iupac.org/analytical_compendium/Cha08sec324.pdf ⇑
19 Einführung in die Instrumentelle Analytik: Elektrochemische Methoden, Orban, O., 2020, Folie 51 ⇑
Monographiebeispiel: Clozapin, Gehaltsbestimmung
Stoffcharakterisierung (Wirkung und Anwendung)
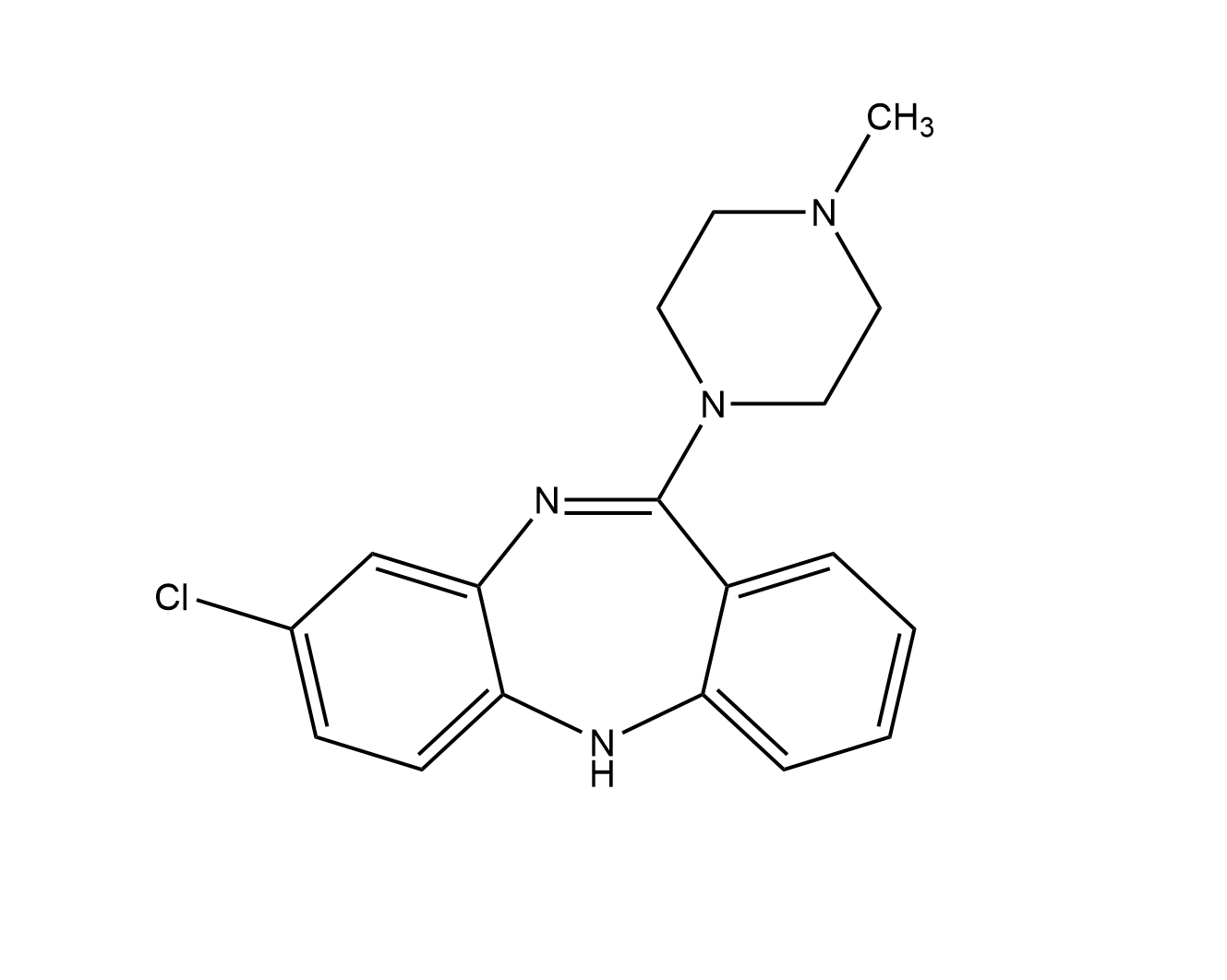
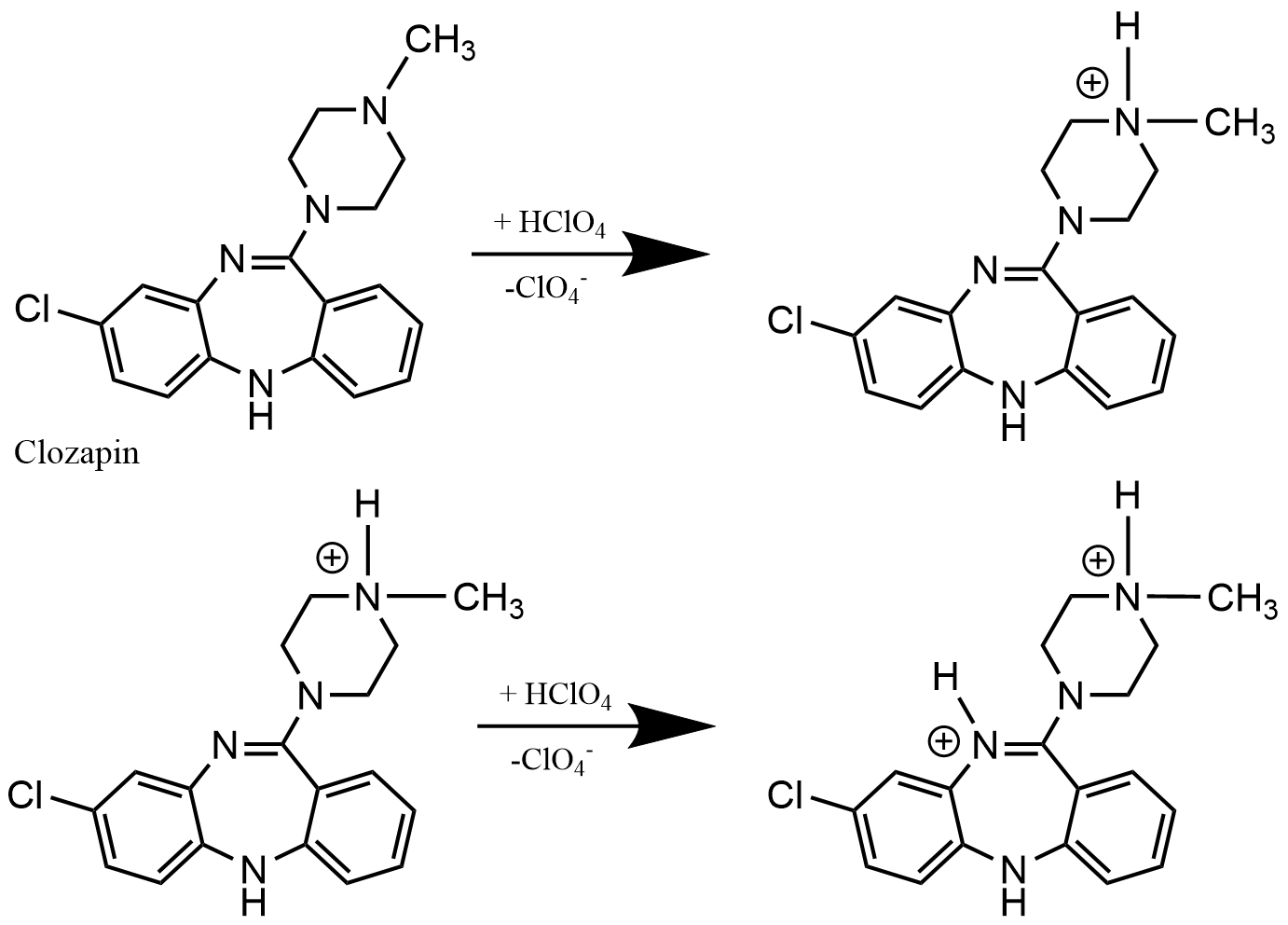
Strukturformel von Clozapin.
Clozapin (8-Chlor-11-(4-methylpiperazin-1-yl)-5H-dibenzo[b,e][1,4]diazepin) ist ein atypisches Neuroleptikum der zweiten Generation aus der Stoffgruppe der Benzodiazepine bzw. Dibenzodiazepine.
Es handelt sich hierbei um ein gelbes, kristallines Pulver, welches in Wasser fast unlöslich ist. Clozapin löst sich in Dichlormethan und Ethanol 96 %. Der Schmelzpunkt liegt zwischen 183 und 184 °C.1
Die neuroleptische Wirkung wird durch die kompetetive Inhibition verschiedener Neurotransmitterrezeptoren hervorgerufen:
Für die neuroleptische bzw. antipsychotische Wirkung ist vor allem die Inhibition von Serotonin- und Dopaminrezeptoren von Bedeutung.
Diese Wirkungen werden vor allem zur Behandlung von therapieresistenter Schizophrenie, seltener zur Therapie von Wahnvorstellungen und Halluzinationen eingesetzt.
Da Clozapin nur 40-60 % der Dopaminrezeptoren im Corpus striatum, einem Basalganglion zur Hemmung von Bewegungsabläufen im Großhirnmark (Extrapyramidalmotorisches System, EPS) hemmt, wird es als bevorzugte Therapieoption bei psychotischen Symptomen von Parkinson- und Chorea-Huntington-Patienten eingesetzt. 3,4
Aufgrund des breiten Wirkungsspektrums treten viele unerwünschte Nebenwirkungen auf, die vor der Anwendung unbedingt abgewogen werden müssen:
- sehr häufig: Schläfrigkeit/Sedierung, Schwindel, Tachykardie, Obstipation (Verstopfung), Hypersalivation (übermäßige Speichelproduktion)
- häufig: Leukopenie, Leukozytose, Gewichtszunahme, Dysarthrie (versch. Sprachstörungen), Konvulsionen, Tremor, Kopfschmerzen, Verschwommensehen, EKG-Veränderungen (Long-QT-Syndrome), Hypotonie, Hypertonie, Übelkeit & Erbrechen, erhöhte Leberenzymwerte, benigne Hyperthermie, Fieber
- gelegentlich: Agranulozytose (erniedrigte Granulozyten-Werte), Dysphemie (Negativassoziationen), malignes neuroleptisches Syndrom (lebensbedrohlich)
- selten: Anämie, Diabetes mellitus, Ruhelosigkeit, Konfusion, Kreislaufkollaps, Arrhythmie, Thromboembolie, Dysphagie, Pankreatitis, Hepatitis
- sehr selten: Thrombozytopenie, Hyperglykämie, Hypercholesterinämie, Zwangsstörung, Kardiomyopathie, Herzstillstand, Atemdepression, Ileus (Darmverschluss), Lebernekrose, Hautreaktionen, Nephritis, plötzlicher Tod 5
Bedingt durch die unerwünschten Arzneimittelwirkungen (UAW) gilt es vor Beginn der Therapie, bestehende Erkrankungen von Leber, Nieren und Herz, sowie eine bestehende Agranulozytose oder Epilepsie auszuschließen (Kontraindikationen). Die Einnahme zusammen mit anderen Benzodiazepinen muss aufgrund eines erhöhten Risikos für Kreislaufzusammenbruch und Atemstillstand überwacht werden.
Clozapin wird aufgrund der drastischen Nebenwirkungen als letzte Therapieoption bei Resistenzen, also Ausbleiben von Therapieerfolgen, gegenüber anderen Therapieoptionen und bei Parkinsonpatienten eingesetzt.
Durchführung der Monographie
Die Monographie von Clozapin umfasst zur Gehaltsbestimmung die Titration mit einer starken Säure im nicht wässrigen Medium, welche sich mittels pH-Elektrode (z.B. Glaselektrode mit SSE als Bezugselektrode) besonders gut potentiometrisch indizieren lässt. Zu beachten ist dabei, dass die pH-Skala ungültig ist und nur für die Endpunkterkennung der Titration eingesetzt wird.
Der Gehalt der Substanz muss laut Europäischem Arzneibuch zwischen 99,0 und 101,0 % liegen.
Die Gehaltsbestimmung wird wie folgt vorgeschrieben:
Auswertung/ Interpretation/ Bedeutung und Eignung der analytischen Methode
Die aus der Durchführung erhaltenen Messwerte werden in einem Koordinatensystem dargestellt, hierbei wird der Verbrauch an Maßlösung (X-Achse) gegen die gemessene Spannung (Y-Achse) aufgetragen. Aus der so entstehenden Titrationskurve kann rechnerisch oder graphisch der Äquivalenzpunkt/ die Äquivalenzpunkte bestimmt werden. Rechnerisch werden die erste und zweite Ableitung der Titrationskurve gebildet, wobei der Äquivalenzpunkt in der ersten Ableitung ein Maximum und in der zweiten Ableitung eine Nullstelle bildet. Vor allem bei undeutlich ausgeprägten Wendepunkten oder zur Automatisierung der Titration bietet sich das rechnerische Verfahren an. Zur graphischen Bestimmung des Äquivalenzpunktes verwendet man zwei unterschiedliche Methoden: Das Tangenten-Verfahren und das Tubbs-Verfahren.
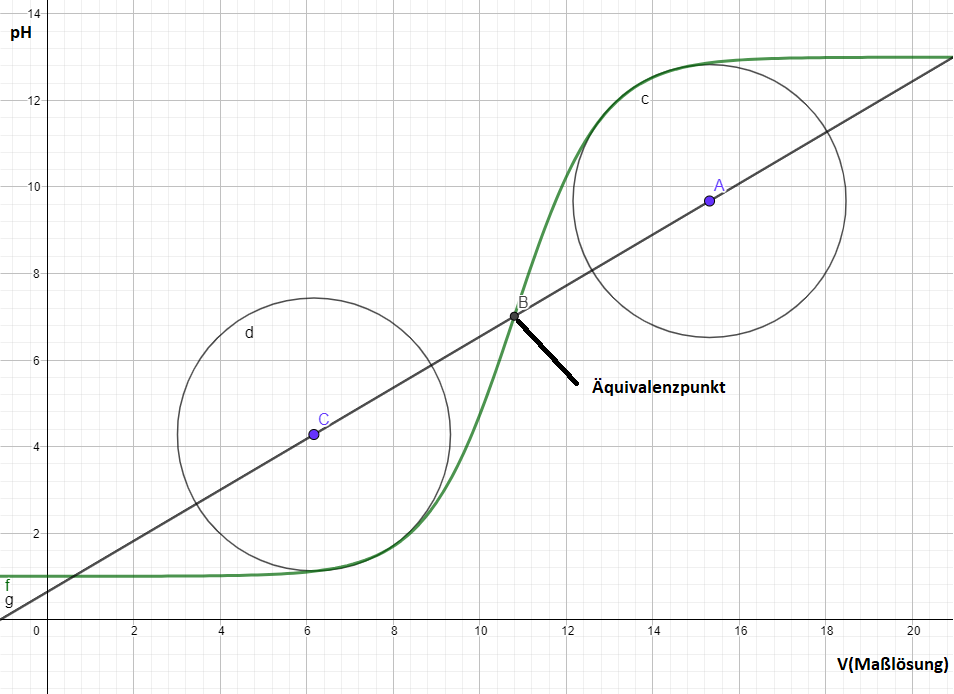
Auswertung potentiometrischer Titrationskurven mittels Tubbs-Verfahren.
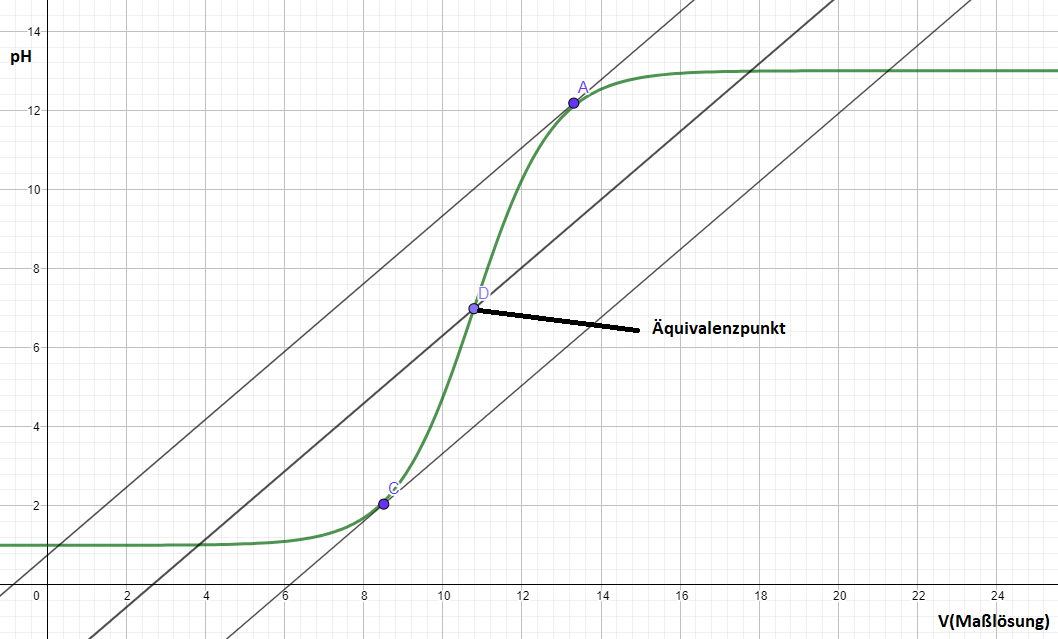
Auswertung potentiometrischer Titrationskurven mittels Tangentenverfahren.
Tangenten-Verfahren: Zur Durchführung des Tangenten-Verfahrens werden parallele Tangenten an die obere und die untere Krümmung der Titrationskurve gelegt. Eine dritte parallele Linie genau in der Mitte der beiden Tangenten zeigt mit ihrem Schnittpunkt mit der Kurve den Äquivalenzpunkt an. Das Verfahren ist recht einfach und eignet sich nur bei symmetrischen Titrationskurven.
Tubbs-Verfahren: Wird bevorzugt bei unsymmetrischen Titrationskurven eingesetzt. Hierbei wird jeweils ein Kreis in die beiden Krümmungen gelegt, der sich genau an die Kurve anschmiegt, etwa mittels Schablonen oder Zirkel. Verbindet man dann die Kreismittelpunkte zeigt der Schnittpunkt der so entstehenden Linie mit der Titrationskurve den Äquivalenzpunkt an.
Eine weitere, etwas aufwendigere Methode ist das Gran-Verfahren. Es eignet sich besonders zur Verbesserung der Genauigkeit bei kleinen Konzentrationen und zum Ausschluss von Messfehlern in der Nähe des Äquivalenzpunktes, indem der Bereich davor und danach linearisiert wird. Dadurch entstehen zwei Geraden, die im Optimalfall beide den gleichen Schnittpunkt mit der X-Achse haben (Nullstelle) und so den Äquivalenzpunkt festlegen. Die Gerade aus den Messpunkten vor dem Äquivalenzpunkt spiegelt dabei die Restmenge des Titranden wieder, während die andere Gerade aus den Messpunkten nach dem Äquivalenzpunkt proportional zur Überschüssigen Maßlösung ist. Die Linearisierung geschieht mittels Gran-Ausdruck, der sich je nach Typ der Titration ändert. 7
Alternativen zur Potentiometrie: Die Gehaltsbestimmung von Clozapin kann auch spektrophotometrisch durchgeführt werden, was in pharmazeutischen Zubereitungen relevant ist, etwa in Tabletten oder der Prozessanalytik. Weitere Bestimmungsmethoden sind die Konduktometrie, die DC und GC sowie die HPLC (auch in Kombination mit Massenspektrometrie). 8,9
Einzelnachweise
1 Ammon, H. P. T. & Schubert-Zsilavecz, M. [Hrsg.](2014). Hunnius Pharmazeutisches Wörterbuch (11., aktualisierte Auflage). Berlin, Boston: Walter de Gruyter. ⇑
2 National Center for Biotechnology Information (2021). PubChem Compound Summary for CID 135398737, Clozapine. Retrieved May 22, 2021, from https://pubchem.ncbi.nlm.nih.gov/compound/Clozapine ⇑
3 https://flexikon.doccheck.com/de/Clozapin. DocCheck Flexikon (Liste der Autoren: https://flexikon.doccheck.com/de/Spezial: Artikel_Autoren/Clozapin?offset=10&limit=10 lizensiert unter CC BY-NC-SA, abgerufen am 22.05.2021 ⇑
4 https://flexikon.doccheck.com/de/Striatum. DocCheck Flexikon (Liste der Autoren: https://flexikon.doccheck.com/de/Spezial:Artikel_Autoren/Striatum, lizensiert unter CC BY-NC-SA, abgerufen am 22.05.2021) ⇑
5 Fachinformation zu Clozapin-ratiopharm® (November 2020). Abgerufen am 23.05.2021, von https://www.fachinfo.de/suche/fi/009863 ⇑
6 Erstellt nach: Rücker, G., Neugebauer, M. & Willems, G. G.(2013). Instrumentelle Pharmazeutische Analytik. Stuttgart, Germany: Wissenschaftliche Verlagsgesellschaft Stuttgart. ⇑
7 Rücker, G., Neugebauer, M. & Willems, G. G.(2013). Instrumentelle Pharmazeutische Analytik. Stuttgart, Germany: Wissenschaftliche Verlagsgesellschaft Stuttgart, S.574ff ⇑
8 Ph. Eur. 10.0/1191 Clozapin ⇑
9 Arzneibuchkommentar 6.0/1191 Clozapin ⇑
TU-Braunschweig Institut für Medizinische und Pharmazeutische Chemie Seminar: Instrumentelle Analytik Kontakt: tubs@t-kellner.de